Learning how to find the area of the shaded region is a fundamental skill in geometry. This process involves analyzing figures, applying the right formulas, and using logical reasoning to calculate the required area. Whether you’re solving academic problems or tackling real-world tasks, mastering this concept is crucial. In this article, we will provide a detailed and SEO-optimized guide to help you calculate the area of shaded regions efficiently.
Introduction
Shaded regions in geometry represent specific parts of a figure that are visually distinguished, often by coloring or patterning, to indicate a focus area. They may represent leftover portions, overlaps, or specific sections of a diagram. For instance, in a circle with a smaller circle inscribed, the shaded region might signify the area between the two. Understanding how to calculate the area of the shaded region is a fundamental skill in geometry that combines critical thinking with mathematical application. Whether in classroom exercises or real-world problems, this concept often involves breaking down complex shapes into simpler ones and applying area formulas strategically.
Understanding Shaded Regions in Geometry
A shaded region in a geometric figure refers to a part of the shape that is visually distinguished, usually through coloring or patterns. To find the area of the shaded region, you need to determine the dimensions of the shapes involved and understand their relationships. Shaded regions commonly appear in composite figures, which are made up of multiple geometric shapes like circles, rectangles, and triangles.
The area of a shaded region is often calculated by subtracting the area of one part of the figure from another or adding areas together when multiple shapes overlap.
Importance of Units in Shaded Area Calculations
Units are crucial in any area calculation, as they provide a standard measure of size and prevent confusion. When finding the area of shaded regions, it’s essential to ensure all dimensions are in the same unit system, such as centimeters, meters, or inches. Mismatched units can lead to incorrect results, which could have real-world consequences, especially in fields like construction or engineering. For example, a miscalculated area in a blueprint could lead to material shortages or overspending. Always express the final area with the correct unit squared (e.g., cm², m²) to ensure clarity and accuracy.
Essential Formulas for Finding Area
To calculate the area of shaded regions, you’ll rely on basic formulas for common geometric shapes. Here’s a quick reference table:
| Shape | Area Formula |
|---|---|
| Rectangle | A=length×widthA = \text{length} \times \text{width}A=length×width |
| Triangle | A=12×base×heightA = \frac{1}{2} \times \text{base} \times \text{height}A=21×base×height |
| Circle | A=πr2A = \pi r^2A=πr2 |
| Semicircle | A=12πr2A = \frac{1}{2} \pi r^2A=21πr2 |
| Trapezoid | A=12(base1+base2)×heightA = \frac{1}{2} (\text{base}_1 + \text{base}_2) \times \text{height}A=21(base1+base2)×height |
These formulas form the foundation for solving any shaded area problem.
Concept of Composite Shapes
Composite shapes are geometric figures made by combining two or more basic shapes, such as rectangles, triangles, circles, or trapezoids. Shaded regions often arise within composite shapes, either as cut-outs, overlaps, or sections needing measurement. For example, a rectangle with a semicircle cut from one edge is a composite shape. To calculate the area of the shaded region in such figures, you use a combination of addition and subtraction. Mastering composite shapes helps in solving more complex problems, as real-world objects often don’t adhere to simple geometric forms. It also lays the groundwork for advanced topics like calculus, where irregular shapes are divided into manageable parts.
How to Find the Area of the Shaded Region
To find the area of the shaded region, follow these steps:
- Analyze the Figure: Identify the shapes that make up the figure and determine the dimensions provided. Recognize whether the shaded region involves subtraction (e.g., a cut-out) or addition (e.g., overlapping areas).
- Apply the Correct Formula: Use the appropriate area formula for each shape. Subtract the area of unwanted parts from the whole or sum areas as needed.
- Perform the Calculation: Carefully compute the areas and use consistent units throughout.
Let’s walk through a couple of examples to understand the process better.
Area Between Two Circles
Imagine a larger circle with a radius of 10 cm and a smaller circle inside it with a radius of 6 cm. The shaded region is the area between these two circles.
- Area of Larger Circle:
A=πr2=3.14×102=314 cm2A = \pi r^2 = 3.14 \times 10^2 = 314 \, \text{cm}^2A=πr2=3.14×102=314cm2 - Area of Smaller Circle:
A=πr2=3.14×62=113.04 cm2A = \pi r^2 = 3.14 \times 6^2 = 113.04 \, \text{cm}^2A=πr2=3.14×62=113.04cm2 - Shaded Area:
314−113.04=200.96 cm2314 – 113.04 = 200.96 \, \text{cm}^2314−113.04=200.96cm2
The area of the shaded region between the circles is 200.96 square centimeters.

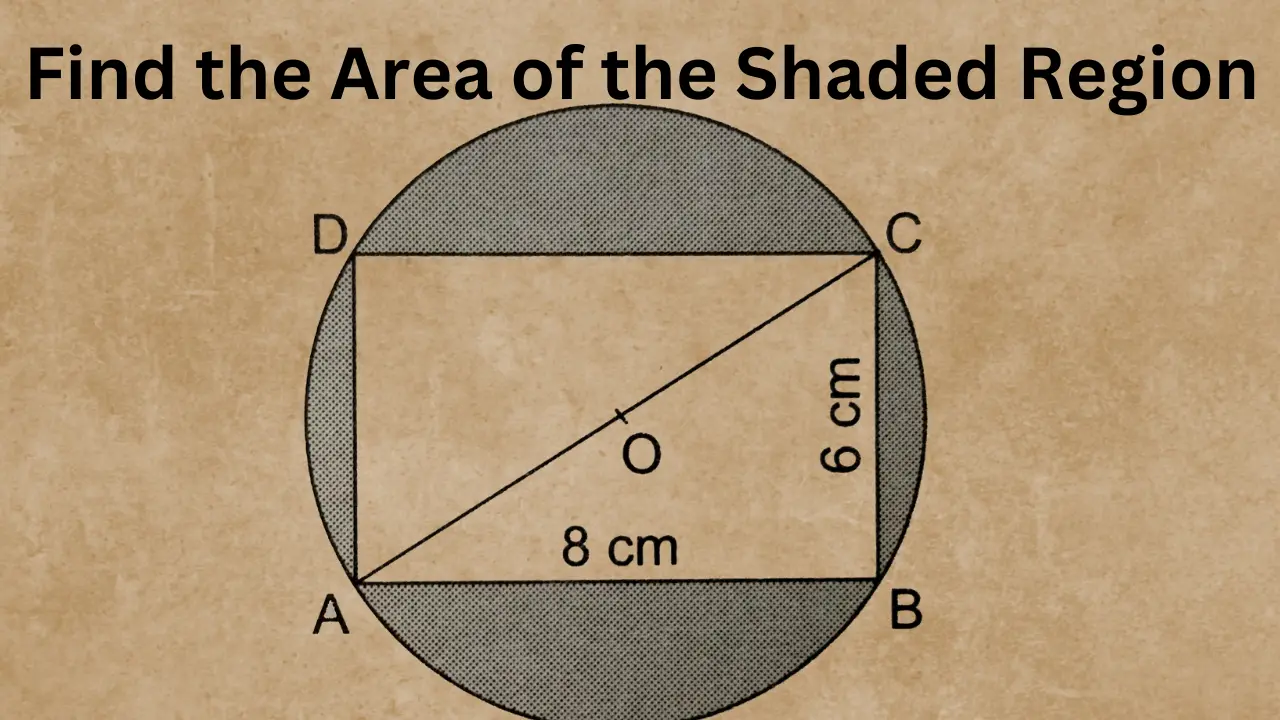
Rectangle with a Triangular Cut-Out
Consider a rectangle measuring 8 cm by 6 cm, with a triangle cut out from one corner. The triangle has a base of 4 cm and a height of 4 cm.
- Area of Rectangle:
A=length×width=8×6=48 cm2A = \text{length} \times \text{width} = 8 \times 6 = 48 \, \text{cm}^2A=length×width=8×6=48cm2 - Area of Triangle:
A=12×base×height=12×4×4=8 cm2A = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 4 \times 4 = 8 \, \text{cm}^2A=21×base×height=21×4×4=8cm2 - Shaded Area:
48−8=40 cm248 – 8 = 40 \, \text{cm}^248−8=40cm2
The shaded area of the remaining rectangle is 40 square centimeters.
Also Read: When to Stop Using Gauze After Wisdom Tooth Extraction
Practical Applications of Finding Shaded Areas
Understanding how to find the area of the shaded region has several real-world applications:
- Architecture and Construction: Shaded areas in blueprints often represent specific materials or zones requiring measurements.
- Landscaping and Gardening: Calculating areas helps in planning layouts for gardens, paths, or decorative features.
- Art and Design: Artists use shaded areas to define proportions or layouts in creative projects.
By mastering this skill, you can apply it in diverse scenarios.
Also Read: When is Julion Alvarez Coming to the USA?
Avoiding Common Mistakes
When solving problems involving shaded areas, students often make errors. Here are some tips to avoid common pitfalls:
- Check Dimensions: Double-check all measurements before starting calculations.
- Use Consistent Units: Always ensure units are uniform across all calculations to avoid mismatched results.
- Analyze the Figure: Spend time understanding the figure’s layout to identify shapes correctly.
Summary of Shaded Region Scenarios
Here’s a quick guide to help you tackle common shaded region problems:
Also Read: When is Q2 2024 What a Financial Quarter is?
| Scenario | Formula |
|---|---|
| Two Circles (Annulus) | A=πR2−πr2A = \pi R^2 – \pi r^2A=πR2−πr2 |
| Rectangle with Cut-Out Shape | A=Rectangle Area−Shape AreaA = \text{Rectangle Area} – \text{Shape Area}A=Rectangle Area−Shape Area |
| Overlapping Shapes (Union) | A=Area1+Area2−Overlap AreaA = \text{Area}_1 + \text{Area}_2 – \text{Overlap Area}A=Area1+Area2−Overlap Area |
Using Technology to Find the Area of Shaded Regions
Technology plays a significant role in making shaded region calculations faster and more accurate. Tools such as geometry software, graphing calculators, and online calculators allow users to input dimensions and obtain results instantly. Programs like AutoCAD or GeoGebra are particularly useful for architects and engineers dealing with complex shapes. For students, apps and interactive tools provide step-by-step solutions, helping them learn the underlying concepts while verifying their answers. Using technology also minimizes errors, ensuring precise results, especially for intricate or irregular shapes that are difficult to calculate manually.
Also Read: Brian Bosworth Seattle Net Worth Football Star to Hollywood Icon
Applications in Real Life
Calculating shaded areas has numerous practical applications in everyday life and professional fields. In architecture, shaded regions might represent unoccupied spaces or areas requiring a specific material. Landscapers use shaded areas to calculate how much ground cover or grass is needed for irregularly shaped gardens. In art and design, measuring shaded regions helps in planning layouts for patterns, murals, or quilts. Engineers often calculate these areas to determine load-bearing capacities or material distribution. By understanding how to find the area of the shaded region, individuals can solve practical problems efficiently and accurately.
Final Thoughts
Learning how to find the area of the shaded region is an essential skill that combines mathematical reasoning with practical problem-solving. By identifying the shapes involved, applying the correct formulas, and avoiding common mistakes, you can confidently solve any problem involving shaded areas. Whether you’re a student tackling a geometry exam or someone applying these skills in the real world, this guide equips you with everything you need to succeed.
Also Read: Fabien Diomande Net Worth 2023 His Life, Career, and Wealth